つくば市研究学園、下妻市、八千代、筑西明野で小中学生・高校生の学力伸ばすなら学習塾のBES塾へ。


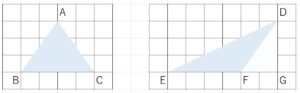
「問題が解ける」と「問題を理解する」。
この2つは一見すると同じように思えます。
しかし、よりハイレベルな学力を身に付けたい場合は、この2つに大きな違いがあることを意識するのが重要です。
その例として、今回は小学5年生の三角形の問題を用意しました。
△ABCと△DEFの面積について考えたとき、この2つの面積は等しいです。
理由は三角形の面積の公式である「底辺×高さ÷2」に関わる底辺と高さがどちらも同じだからです。
しかし、△DEFは底辺がEF、高さがDGとそれぞれ隣接していない長さを計算に使用します。
△ABCとは形が大きく違うように見えますが、この場合も同じ公式で求めることができます。
そのことを不思議に思った経験はありますでしょうか。
では、どうして△DEFのような形でも「底辺×高さ÷2」で求まるのか理由を説明できるでしょうか。
小学5年生の算数の教科書で実際に載っていた問題ですが、意外と答えるのは大人でも難しいのではないでしょうか。
「問題が解ける」人は、「底辺×高さ÷2」の公式に当てはめて計算すれば答えは出せます。
しかし、多くの場合はなぜそれで求まるのかを答えることができません。
その理由までを理解していないからです。
基本問題を解くだけならそれでもいいのですが、ハイレベルな問題では工夫や発想力が問われるため、こういった根底の部分まで理解できているかが差になってくるものです。
今回の問題の解法の1例です。
まず、△DEF=△DEG-△DFGとして考えます。
それぞれの三角形を公式に当てはめた場合は、
(EG×DG÷2) - (FG×DG÷2) になります。
ここで、×DG÷2は共通している計算部分ですから、小学生の計算の工夫で習う
○×□-△×□=(○-△)×□ の形に合わせると、
(EG-FG)×DG÷2 というように式変形ができます。
最後にEG-FG=EFですから、
EF×DG÷2 という式が導けます。
よって、△DEFのような形でも「底辺×高さ÷2」が成り立つのです。
ちなみに小学校の教科書では次のように説明していました。
△DEFと合同な三角形△D’E’F’を用意します。
△D’E’F’を180°回転させて、辺DEとE’D’が重なるようにします。
すると、平行四辺形F’EFDができます。
平行四辺形の面積は「底辺×高さ」で求まり、この平行四辺形は本来の三角形の面積の2倍なので、「底辺×高さ÷2」で△DEFの面積が求まるというものです。
普段の勉強でふと「なぜ? どうして?」といった疑問が浮かんだとき、それをとことん突き詰めてみるというのは重要です。
同じ学校で同じ授業を受けていたとしても、そういった深いところまで考えるかどうかが、学力の大きな差となって表れてくるものだと思います。
